밝기 변환 함수들(intro, 영상 네거티브, 로그 변환)

밝기 변환은 영상 처리 기법 중 가장 간단한 축에 든다. 처리 전후의 화소 값들이 각각 r과 s로 표기된다. 앞 절에서 언급했듯이, 이 값들은 s = T(r) 형태의 식에 의해 관련되며, 여기서 T는 화소 값 r을 화소 값 s로 매핑하는 변환이다. 디지털 수량을 다루고 있으므로, 변환 함수의 값은 일반적으로 1-D 배열에 저장되며, r에서 s로의 매핑은 테이블 룩업(표 검색)에 의해 구현된다. 8비트 환경에서 T의 값들을 담고 있는 룩업 테이블은 256개의 요소를 가질 것이다.

밝기 변환에 대한 소개로서, 영상 개선을 위해 자주 사용되는 세 가지 기본 함수 유형을 보여주는 아래 그림을 보자:선형(네거티브 및 항등 변환들), 로가리듬(로그 및 역-로그 변환들), 거듭제곱 법칙(또는 멱승법칙, n차 거듭제곱 및 n차 제곱근 변환들). 항등 함수는 출력 밝기가 입력 밝기와 같은 사소한 경우이다. 그래프에는 단순히 완성을 위해 포함되어 있다.

 

영상 네거티브

밝기 레벨의 범위가 [0, L-1]인 영상의 네거티브는 다음 식에 의해 주어지는 네거티브 변환에 의해 만든다:

 

 

이런 방식으로 영상의 밝기 레벨을 반진시키면 사진 네거티브와 똑같은 것을 만든다. 이 유형의 처리는 특히 흑색 영역의 면적 비중이 클 때, 영상의 어두운 영역에 놓여 있는 흰색이나 그레이 디테일을 개선시키는 데 특히 적합하다.

 

 

로그 변환

로그 변환의 일반형은 아래 식과 같다.

 

 

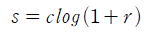
여기서 c는 상수이며, r≥0 으로 가정된다. 로그 곡선의 모양은 이 변환이 입력의 낮은 밝기 값들의 좁은 범위를 넓은 범위의 출력 레벨들로 매핑한다는 것을 보여준다. 높은 값의 입력 레벨들에 대해서는 그 반대이다. 입력의 어두운 화소들의 값들을 신장시키고, 높은 레벨의 값들을 압축하고자 할 때 이런 변환을 사용한다. 역 로그 변환은 그 반대이다.

일반 로그 함수 모양을 갖는 곡선이라면 이 영상 밝기 레벨 신장/압축을 달성할 것이나, 이후에 다룰 거듭제곱 법칙 변환이 이 목적을 위해 훨씬 더 유연하다. 로그 함수는 화소 값들의 편차가 큰 영상의 동적 범위를 압축하는 중요한 특성을 가진다. 0부터 10^6이나 그 이상까지 변하는 스펙트럼 값들을 흔하게 접할 수 있다. 이런 숫자들을 처리하는 것이 컴퓨터에 아무런 문제가 되지 않겠지만, 영상 표시 시스템들은 일반적으로 그렇게 넓은 범위의 밝기 값들을 충실하게 표현할 수 없다. 그 결과, 일반적 Fourier 스펙트럼을 표시할 때 밝기 디테일의 상당 부분이 손실될 수 있다.

 

 

로그 변환의 예로서 위 그림처럼 0에서 1.5 × 10^6 범위의 값을 갖는 Fourier 스펙트럼이 있다고 가정한다. 이 값들이 8비트 표시기를 위해 선형적으로 스케일링될 때, 스펙트럼의 가장 밝은 값의 화소들이 더 낮은 (그리고 똑같이 중요한) 값들을 희생하여 표시기를 차지할 것이다. 이 패권의 효과는 위 그림 영상에서 흑색으로 나타나지 않은 상대적으로 작은 영역이 생생하게 보여준다. 이 밝기 값들을 이 방식으로 표현하는 대신에 로그 변환식을 스펙트럼 값들에 먼저 적용하면(위 그림은 c=1일 경우), 결과 값들의 범위는 더 다루기 쉬운 0에서 6.2가 된다. 우측 그림이 새 범위를 선형적으로 스케일링해서 똑같은 8비트 표시기에 스펙트럼을 표시한 결과를 보여준다. 수정되지 않은 스펙트럼 표시와 비교할 때 이 영상에서는 풍부한 디테일을 볼 수 있다. 영상 처리 문헌들에서 볼 수 있는 Fourier 스펙트럼의 대부분은 바로 이런 방식으로 스케일링되어 있다.