밝기 변환 함수(구간 선형 변환)

이전 게시글에서 논의한 함수 유형들에 대한 구간 선형 함수의 중요한 장점은 구간 함수들의 형태가 임의로 복잡해질 수 있다는 것이다. 사실상, 어떤 중요한 변환들은 실질적 구현이 구간 함수들로서만 공식화될 수 있다. 구간 함수의 중요한 단점은 그것을 규정하는 데 사용자 입력이 훨씬 더 많이 필요하다는 것이다.

 

콘트라스트 스트레칭

가장 간단한 구간 선형 함수 중 하나는 콘트라스트-스트레칭 변환이다. 낮은 콘트라스트 영상의 원인은 나쁜 조명, 영상화 센서의 좁은 동적 범위, 영상 획득 시 잘못된 조리개 설정 등일 수 있다. 콘트라스트 스트레칭은 영상의 밝기 레벨 범위를 넓혀서 기록 매체나 표시 장치의 전체 밝기 범위를 사용하게 하는 것이다.

그림 (a)가 콘트라스트 스트레칭에 사용되는 전형적인 변환을 보여준다. 점 (r1, s1)과 (r2, s2)의 위치가 변환 함수의 모양을 제어한다. 만일 r1=s1, r2=s2이면, 그 변환은 밝기 레벨에 아무런 변화를 주지 않는 선형 함수이다. 만일 r1=r2, s1=0, s2=L-1 이면, 그 변환은 그림 (b)가 보여주듯이 이진 영상을 만드는 문턱치 처리 함수가 된다. 그 사이의 (r1, s1)과 (r2, s2) 값들은 출력 영상의 밝기 레벨들이 분포되는 정도를 다양하게 만들어서 콘트라스트에 영향을 준다. 일반적으로 r1≤r2, s1≤s2 로 가정되므로 이 함수는 단일 값을 가지며 단조 증가한다. 이 족너이 밝기 레벨의 순서를 유지하므로, 처리된 영상에서 인위적 밝기 구조(intensity artifacts)가 생기는 것을 방지한다.

그림(b)는 낮은 콘트라스트를 갖는 8비트 영상을 보여준다. 그림(c)가 (r1,s1) = (rmin, 0), (r2,s2) = (rmax, L-1)로 설정해서 얻은 콘트라스트 스트레칭의 결과를 보여준다. 여기서 rmin과 rmax는 각각 영상의 최소 및 최대 밝기 레벨을 나타낸다. 따라서 이 변환 함수가 레벨들을 원래 범위에서 최대 범위[0, L-1]로 선형적으로 스트레칭하였다. 끝으로 그림(d)가 앞에서 정의된 문턱치 처리 함수를 사용한 결과를 보여주는데, 이때 (r1,s1) = (m,0), (r2,s2)=(m, L-1) 이었다. 여기서 m은 영상의 평균 밝기 레벨이다. 이 결과들이 비롯된 원래 영상은 약 700배로 확대된 꽃가루의 SEM(주사형 전자 현미경) 영상이다.

 

밝기 레벨 슬라이싱

 

영상의 특정 밝기 범위를 강조하는 게 자주 필요하다. 그 응용에는 인공위성 영상에서 물이 모여 있는 곳과 같은 특징들을 강조하기, X-선 영상에서의 결함을 강조하기 등이 해당된다. 흔히 밝기-레벨 슬라이싱(intensity-level slicing) 이라고 불리는 이 프로세스는 몇 가지 방법으로 구현될 수 있으나, 대부분 두 가지 기본형이 변형된 것들이다. 한 방법은 관심 영역에 드는 모든 값들을 한 값(예: 흰색)으로 표시하고, 나머지 밝기 값들을 다른 값(예: 흑색)으로 표시하는 것이다. 왼쪽 그림이 보여주는 이 변환은 이진영상을 만든다. 두 번째 접근법은 오른쪽 그림의 변환에 기반하며, 원하는 밝기 범위를 밝게(또는 어둡게) 만들고, 영상의 남저ㅣ 밝게 레벨들은 모두 그대로 놔둔다

 

 

비트-평면 슬라이싱

화소는 비트들로 구성된 디지털 수이다. 예를 들면 256-레벨 그레이-스케일 영상에서 각 화소의 밝기는 8비트(1바이트)로 구성된다. 밝기-레벨 범위를 강조하는 대신에, 전체 영상 모양에 대한 특정 비트의 기여를 강조할 수 있다. 아래 그림에서 보여주듯이 8비트 영상은 8개의 1비트 평면들로 구성된 것으로 간주될 수 있다: 평면 1은 영상의 모든 화소들의 최하위 비트를 담고 있으며, 평면 8은 모든 최상위 비트들을 담고 있다.

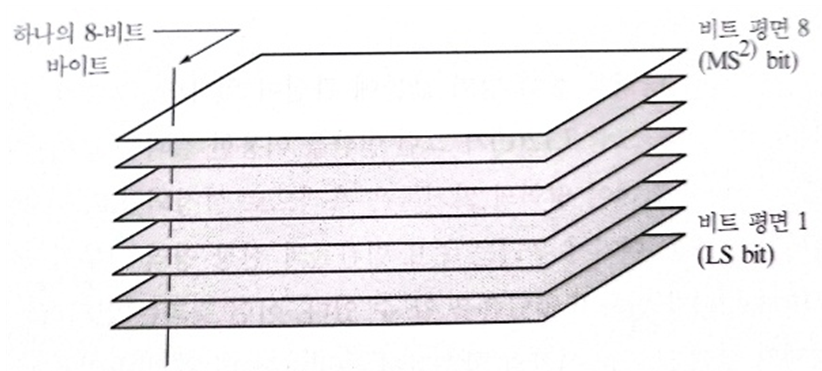
8비트 영상의 비트 평면 표현

 

 

 

 

아래 그림 (a)는 8비트 그레이 스케일 영상을 보여주며, 그림 (b)부터 (i)까지는 8개의 1비트 평면들을 보여준다:

그림 (b)가 취하위 비트에 해당한다. 네 개의 상위 비트 평면들, 특히 끝의 두 개가 시각적으로 중요한 데이터의 상당량을 담고 있음을 주시한다. 하위 평면들은 영상의 더 미세한 밝기 디테일에 기여한다. 원래 영상에는 밝기 값이 194인 회색 경계가 있다. 일부 비트 평면의 해당 경게는 흑색(0)이고 다른 것들은 백색(1)임을 주목한다. 그 이유를 알아 보기 위해 그림 (a)의 아래쪽 경계의 중간에 있는 화소를 고찰하자. 최상위 평면부터 시작해서 비트 평면들의 해당 화소들의 값은 1 1 0 0 0 0 1 0이다. 이 값은 십진수 194의 이진수 표현이다. 원래 영상의 모든 화소 값은 비트 평면들의 해당 이진 값 화소들로부터 마찬가지로 복구될 수 있다. 8비트 영상의 8번째 비트 평면에 대한 이진 영상이, 0부터 127 사이의 밝기들은 0으로 매핑하고 128에서 255 사이의 모든 레벨들은 1로 매핑하는 밝기 문턱치 처리 변환 함수로 입력 영상을 처리해서 얻어질 수 있음을 증명하는 것은 어렵지 않다. 그림 (i)의 이진 영상을 바로 이 방식으로 얻었다.

 

 

영상을 비트 평면으로 분해하는 것은 영상에서의 각 비트의 상대적 중요성을 분석하는데 유용하다. 이 프로세스는 영상 양자화에 사용되는 비트 수의 적절성을 판단하는 데 도움이 된다. 또한 이 유형의 분해는 일부 평면만 영상 복구에 사용되는 영상 압축에 유용하다. 예를 들면, 그림 (가)는 비트 평면 8과 비트 평면 7을 사용해서 복구된 영상이다. 이 복구는 n번째 평면의 화소들을 상수 2^(n-1)로 곱해서 수행된다. 이것은 바로 n번째 MS 비트를 십진수로 전환하는 것이다. 사용된 각 평면이 해당 상수로 곱해지며, 사용된 모든 평면들이 더해져서 그레이 스케일 영상이 얻어진다. 따라서 그림 (가)를 얻기 위해 비트 평면 8을 128로, 비트 평면 7을 64로 각각 곱하고, 두 평면을 더했다. 비록 원래 영상의 주요 특징들이 복원되었지만, 복구된 영상은 단조로워 보이고, 특히 배경에서 그러하다. 이것은 두 평면이 겨우 네 개의 서로 다른 밝기 레벨들만을 만들 수 있기 때문에 놀라운 일이 아니다. 이 복구에 비트 평면 6을 더하면 그림 (나)가 보여주듯이 상황이 개선된다. 이 영상의 배경에 눈에 띄는 허위 등고선이 있음을 주목한다. 이 효과는 그림 (다)가 보여주듯이 다섯 번째 비트 평면을 더함으로써 현저히 축소되었다. 이 복구에 다른 평면을 더 사용한다고 해도 현저한 변화는 없을 것이다. 따라서 네 개의 최상위 비트 평면들을 저장하면 만족할 만한 디테일을 갖게 원래 영상을 복구 할 수 있다고 결론 지을 수 있다. 또한, 원래 영상 대신에 이 네 개의 평면을 저장하면 저장 공간이 50% 절약된다(메모리 구조 이슈는 다루지 않음.)